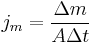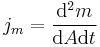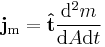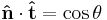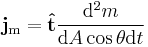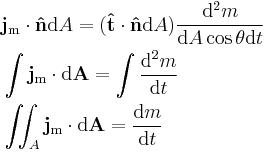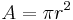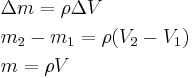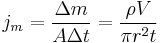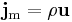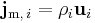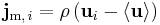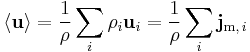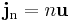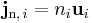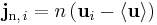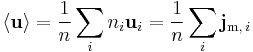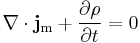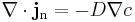Mass flux

In Physics and Engineering, mass flux is the rate of mass flow per unit area. The common symbols are j, J, φ, or Φ (Greek lower or capital Phi), sometimes with subscript m to indicate mass is the flowing quantity. Its SI units are kg s^-1 m^-2. Mass flux can also refer to an alternate form of flux in Fick's law that includes the molecular mass, or in Darcy's law that includes the mass density.^[1]

Unfortunately, sometimes the defining equation for mass flux in this article is used interchangeably with the defining equation in mass flow rate. For example, Fluid Mechanics, Schaum's et al ^[2] uses the definition of mass flux as the equation in the mass flow rate article.

1 Definition
- 1.1 Example
2 Equations for fluids
- 2.1 Alternative equation
- 2.2 Mass and molar fluxes for composite fluids
  - 2.2.1 Mass fluxes
  - 2.2.2 Molar fluxes
3 Usage
4 See also
5 References

Definition

Mathematically, mass flux is defined as:

$j_m = \frac{\Delta m}{ A \Delta t}$

where:

j_m = mass flux,
Δm = change in mass flowing through the area,
Δt = time interval of mass flow.
A = area through which the mass flows through,

In the limit Δm, Δt and A become infinitesimally small, the algebraic definition becomes a calculus definition:

$j_m = \frac{{\rm d}^2 m}{{\rm d}A{\rm d}t}$

Depending on context, mass flux may be treated as a scalar or vector, in practice most usually a vector since all the situation is in three dimensions. The above equation defines j_m as a scalar, it can be made into a vector by introducing a unit vector tangential to the flow, 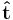$\bold{\hat{t}}$ :

$\bold{j}_{\rm m} = \bold{\hat{t}}\frac{{\rm d}^2 m}{{\rm d}A{\rm d}t}$

The change is the amount that flows after crossing the boundary for some time duration, not simply the initial amount of mass at the boundary minus the final amount at the boundary, since the change in mass flowing through the area would be zero for steady flow.

The area required to calculate the mass flux is real or imaginary, flat or curved, either as a cross-sectional area or a surface. E.g. for substances passing through a filter or a membrane, the real surface is the (generally curved) surface area of the filter, macroscopically - ignoring the area spanned by the holes in the filter/membrane. The spaces would be cross-sectional areas. For liquids passing through a pipe, the area is the cross-section of the pipe, at the section considered. The vector area is a combination of the magnitude of the area through which the mass passes through, A, and a unit vector normal to the area, 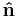$\bold{\hat{n}}$ . 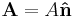The relation is $\bold{A} = A \bold{\hat{n}}$ .

All previous equations are only valid if the flux is normal to the cross-section. In the case the flux (in direction 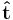$\bold{\hat{t}}$ ) passes through the area at an angle θ to the area normal (in direction 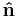$\bold{\hat{n}}$ ), it follows that

$\bold{\hat{n}}\cdot\bold{\hat{t}}= \cos\theta$

(which is the dot product of the unit vectors). The previous equation has a simple modification. The component of flux passing through the area, i.e. normal to the area, is 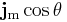$\bold{j}_{\rm m} \cos\theta$ . The component of flux passing tangential to the area is 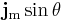$\bold{j}_{\rm m} \sin\theta$ , but there is no flux actually passing through the area, so the this must be zero. The only component of flux passing normal to the area is the cosine component. It follows that the most general equation is:

$\bold{j}_{\rm m} = \bold{\hat{t}}\frac{{\rm d}^2 m}{{\rm d}A\cos\theta{\rm d}t}$

Mass flux is clearly related to mass flow rate in the following way, by taking the dot product of the previous equation with the vector area, then integrating both sides (note the factors of 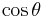$\cos\theta$ cancel):

$\begin{align} & \bold{j}_{\rm m} \cdot \bold{\hat{n}}{\rm d}A = (\bold{\hat{t}}\cdot \bold{\hat{n}}{\rm d}A)\frac{{\rm d}^2 m}{{\rm d}A\cos\theta{\rm d}t} \\ & \int \bold{j}_{\rm m} \cdot {\rm d}\bold{A} = \int \frac{{\rm d}^2 m}{{\rm d}t} \\ & \iint_A \bold{j}_{\rm m} \cdot {\rm d}\bold{A} = \frac{{\rm d} m}{{\rm d}t} \\ \end{align}$

(when integrating on both sides, on the left was for the area dA, on the right with respect to the infinitesimal mass dm) where the integral is evaluated over the area A. This final quantity is the mass flow rate, rate of flow of mass per unit time.

Example

Consider a pipe of flowing water. Suppose the pipe has a constant cross section and we consider a straight section of it (not at any bends/junctions), and the water is flowing steadily at a constant rate, under standard conditions. The area A is the cross-sectional area of the pipe. Suppose the pipe has radius r = 2 cm = 2 × 10^-2 m. The area is then

$A = \pi r^2$

To calculate the mass flux j_m (magnitude), we also need the amount of mass of water transferred through the area and the time taken. Suppose a volume V = 1.5 L = 1.5 × 10^-3 m³ passes through in time t = 2 s. Assuming the density of water is ρ = 1000kg m^-3, we have:

$\begin{align} & \Delta m = \rho \Delta V \\ & m_2 - m_1 = \rho ( V_2 - V_1) \\ & m = \rho V \\ \end{align}$

(since initial volume passing through the area was zero, final is V, so corresponding mass is m), so the mass flux is

$j_m = \frac{\Delta m}{ A \Delta t} = \frac{\rho V}{ \pi r^2 t}$

substituting the numbers gives:

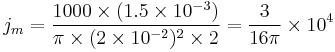
$j_m = \frac{1000 \times (1.5 \times 10^{-3})}{ \pi \times (2 \times 10^{-2})^2 \times 2} = \frac{3}{16\pi}\times 10^4$

which is approximately 596.8 kg s^-1 m^-2.

Equations for fluids

Alternative equation

Using the vector definition, mass flux is also equal to: ^[3]

$\bold{j}_{\rm m} = \rho \mathbf{u}$

where:

ρ = mass density,
u = velocity field of mass elements flowing (i.e. at each point in space the velocity of an element of matter is some velocity vector u).

Sometimes this equation may be used to define j_m as a vector.

Mass and molar fluxes for composite fluids

Mass fluxes

In the case fluid is not pure, i.e. is a mixture of substances (technically contains a number of component substances), the mass fluxes must be considered separately for each component of the mixture.

When describing fluid flow (i.e. flow of matter), mass flux is appropriate. When describing particle transport (movement of a large number of particles), it is useful to use an analogous quantity, called the molar flux.

Using mass, the mass flux of component i is:

$\bold{j}_{{\rm m}, \, i} = \rho_i \mathbf{u}_i$

The barycentric mass flux of component i is

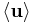$\bold{j}_{{\rm m}, \, i} = \rho \left ( \mathbf{u}_i - \langle \mathbf{u} \rangle \right )$

where $\langle \mathbf{u} \rangle$ is the average mass velocity of all the components in the mixture, given by:

$\langle \mathbf{u} \rangle = \frac{1}{\rho}\sum_i \rho_i \mathbf{u}_i = \frac{1}{\rho}\sum_i \mathbf{j}_{{\rm m}, \, i}$

where :

ρ = mass density of the entire mixture,
ρ_i = mass density of component i,
u _i = velocity of component i.

The average is taken over the velocities of the components.

Molar fluxes

If we replace density ρ by the number of moles n, we have the molar flux analogues.

The molar flux is the number of moles per unit time per unit area, generally:

$\bold{j}_{\rm n} = n \mathbf{u}$

So the molar flux of component i is (number of moles per unit time per unit area):

$\bold{j}_{{\rm n}, \, i} = n_i \mathbf{u}_i$

and the barycentric molar flux of component i is

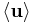$\bold{j}_{{\rm n}, \, i} = n \left ( \mathbf{u}_i - \langle \mathbf{u} \rangle \right )$

where $\langle \mathbf{u} \rangle$ this time is the average molar velocity of all the components in the mixture, given by:

$\langle \mathbf{u} \rangle = \frac{1}{n}\sum_i n_i \mathbf{u}_i = \frac{1}{n}\sum_i \mathbf{j}_{{\rm m}, \, i}$

Usage

Mass flux appears in some equations in hydrodynamics, in particular the continuity equation:

$\nabla\cdot\bold{j}_{\rm m} %2B \frac{\partial \rho}{\partial t}=0$

which is a statement of the mass conservation of fluid. In hydrodynamics, mass can only flow from one place to another.

Molar flux occurs in Fick's first law of diffusion:

$\nabla\cdot\bold{j}_{\rm n} = -D \nabla c$

where D is the diffusion coefficient and c is the concentration of substance.

References

^ "Thesaurius: Mass flux". http://thesaurus.maths.org/mmkb/entry.html?action=entryById&id=2113. Retrieved 2008-12-24.
^ Fluid Mechanics, M. Potter, D.C. Wiggart, Schuam's outlines, McGraw Hill (USA), 2008, ISBN 978-0-07-148781-8
^ Vectors, Tensors, and the basic Equations of Fluid Mechanics, R. Aris, Dover Publications, 1989, ISBN(10) 0-486-66110-5